英文原文:
3 Machine Learning Algorithms You Need to Know
假定有一些数据相干的问题亟待你处理。在此之前你传闻过机械进修算法可以协助处理这些问题,因而你想借此时机测验考试一番,却苦于在此范畴没有任何经历或常识。 你Start谷歌一些术语,如“机械进修模子”和“机械进修办法论”,但一段工夫后,你发明本人完整迷失在了分歧算法之间,因而你预备放弃。
冤家,请保持下去!
侥幸的是,在这篇文章中我将引见三大类的机械进修算法,针对大范畴的数据科学问题,置信你都能满怀自负去处理。
在接下来的文章中,我们将会商决议计划树、聚类算法和回归,指出它们之间的差别,并找出怎么为你的案例选择最适宜的模子。
有监视的进修 vs. 无监视的进修
了解机械进修的根底,就是要学会对有监视的进修和无监视的进修实行分类,由于机械进修中的任何一个问题,都属于这两大类的范围。
在有监视进修的状况下,我们有一个数据集,它们将作为输出供给给一些算法。但条件是,我们曾经晓得准确输出的格局应当是甚么模样(假定输出和输出之间存在一些关系)。
我们随后将看到的回归和分类问题都属于这个种别。
另外一方面,在我们不晓得输出应当是甚么模样的状况下,就应当运用无监视进修。现实上,我们需求从输出变量的影响未知的数据中推导出准确的构造。聚类问题是这个种别的首要代表。
为了使上面的分类更明晰,我会罗列一些实践的问题,并试着对它们实行响应的分类。
示例一
假定你在运营一家房地产公司。思索到新居子的特征,你要依据你之前记载的其他衡宇的发卖量来猜测它的售价是几多。你输出的数据集包含多个屋子的特征,比方洗手间的数目和巨细等,而你想猜测的变量(凡是称为“目的变量”)就是价钱。猜测衡宇的售价是一个有监视进修问题,更确实地说,是回归问题。
示例二
假定一个医学试验的目标是猜测一个人能否会由于一些体质丈量和遗传招致近视水平加深。在这类状况下,输出的数据集是这个人的体质特点,而目的变量有两种:
1 表现可能加深近视,而 0 表现不太可能。猜测一个人能否会加深近视也是一个有监视进修问题,更确实地说,是分类问题。
示例三
假定你的公司具有非常多客户。依据他们比来与贵公司的互动状况、他们近期购置的产品和他们的生齿统计数据,你想要构成类似主顾的群体,以便以分歧的方法应对他们 - 例如向他们中的一些人供给独家扣头券。在这类状况下,你将运用上述说起的特点作为算法的输出,而算法将决议应当构成的组的数目或种别。这明显是一个无监视进修的例子,由于我们没有任何干于输出会怎么的线索,完整不晓得后果会如何。
接下来,我将引见一些更详细的算法......
回归
起首,回归不是一个单一的监视进修技术,而是一个非常多技术所属的完好种别。
回归的首要思惟是给定一些输出变量,我们要猜测目的值。在回归的状况下,目的变量是延续的 - 这意味着它可以在指定的范畴内取任何值。另外一方面,输出变量可所以团圆的也能够是延续的。
在回归技术中,最盛行的是线性回归和逻辑回归。让我们细心研讨一下。
线性回归
在线性回归中,我们测验考试在输出变量和目的变量之间构建一段关系,并将这类关系用条直线表现,我们凡是将其称为回归线。
例如,假定我们有两个输出变量 X1 和 X2,另有一个目的变量 Y,它们的关系可以用数学公式表现以下:
Y = a * X1 + b*X2 +c
假定 X1 和 X2 的值已知,我们需求将 a,b 和 c 实行调剂,从而使 Y 能尽量的靠近真实值。
举个例子!
假定我们具有有名的 Iris 数据集,它供给了一些办法,能经过花朵的花萼巨细和花瓣巨细判别花朵的种别,如:Setosa,Versicolor 和 Virginica。
运用 R 软件,假定花瓣的宽度和长度已给定,我们将施行线性回归来猜测萼片的长度。
在数学上,我们会经过以下公式来获得 a、b 值:
其它翻译版本 (1)
加载中
SepalLength = a * PetalWidth + b* PetalLength +c
响应的代码以下所示:
# Load required packages
library(ggplot2)
# Load iris dataset
data(iris)
# Have a look at the first 10 observations of the dataset
head(iris)
# Fit the regression line
fitted_model <- lm(Sepal.Length ~ Petal.Width + Petal.Length, data = iris)
# Get details about the parameters of the selected model
summary(fitted_model)
# Plot the data points along with the regression line
ggplot(iris, aes(x = Petal.Width, y = Petal.Length, color = Species)) +
geom_point(alpha = 6/10) +
stat_smooth(method = "lm", fill="blue", colour="grey50", size=0.5, alpha = 0.1)
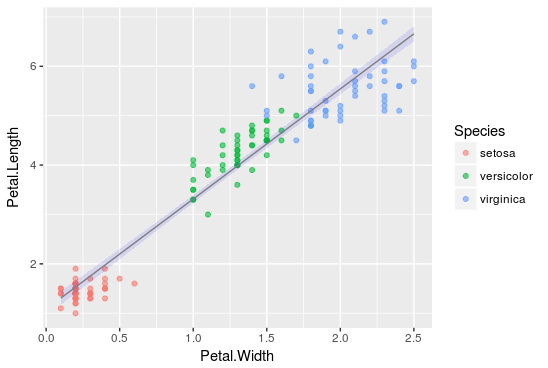
线性回归的后果显示鄙人列图表中,此中斑点表现初始数据点,蓝线表现拟合回归直线,由此得出预算值:a= -0.31955,b = 0.54178 和 c = 4.19058,这个后果可能最靠近实践值,即花萼的真实长度。
接下来,只需将花瓣长度和花瓣宽度的值使用到定义的线性关系中,就能够对花萼长度实行猜测了。
逻辑回归
首要思惟与线性回归完整类似。分歧点是逻辑回归的回归线不再是直的。
我们要树立的数学关系是以下方式的:
Y=g(a*X1+b*X2)
g() 是一个对数函数。
依据该逻辑函数的性质,Y 是延续的,范畴是 [0,1],可以被说明为一个事情发作的几率。
再举个例子!
这一次我们研讨 mtcars 数据集,包括 1973-1974 年间 32 种汽车制作的汽车设计、十特性能目标和油耗。
运用 R,我们将在丈量 V/S 和每英里油耗的根底上猜测汽车的变速器是主动(AM = 0)仍是手动(AM = 1)的几率。
am = g(a * mpg + b* vs +c):
# Load required packages
library(ggplot2)
# Load data
data(mtcars)
# Keep a subset of the data features that includes on the measurement we are interested in
cars <- subset(mtcars, select=c(mpg, am, vs))
# Fit the logistic regression line
fitted_model <- glm(am ~ mpg+vs, data=cars, family=binomial(link="logit"))
# Plot the results
ggplot(cars, aes(x=mpg, y=vs, colour = am)) + geom_point(alpha = 6/10) +
stat_smooth(method="glm",fill="blue", colour="grey50", size=0.5, alpha = 0.1, method.args=list(family="binomial"))
以下图所示,此中斑点代表数据集的初始点,蓝线代表闭合的对数回归线。估量 a = 0.5359,b = -2.7957,c = - 9.9183
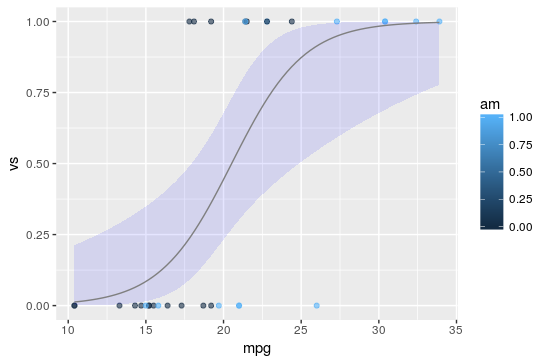
我们可以察看到,和线性回归一样,对数回归的输出值回归线也在区间 [0,1] 内。
关于任何新汽车的丈量 V/S 和每英里油耗,我们可以猜测这辆汽车将运用主动变速器。这是否是精确得吓人?
决议计划树
决议计划树是我们要研讨的第二种机械进修算法。它们被分红回归树和分类树,因而可以用于监视式进修问题。
无能否认,决议计划树是最直观的算法之一,由于它们模拟人们在大多数状况下的决议计划方法。他们根本上做的是在每种状况下绘制一切可能途径的“舆图”,并给出响应的后果。
图形表现有助于更好天文解我们正在讨论的内容。
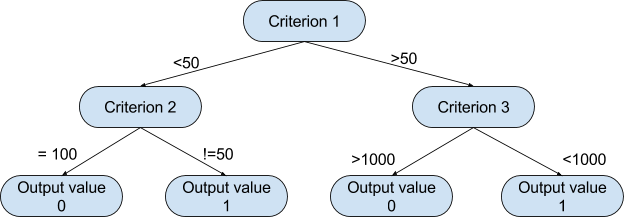
基于像上面如许的树,该算法可以依据响应规范中的值来决议在每一个步调要采取的途径。算法所选择的划分规范和每一个级此外响应阈值的战略,取决于候选变量关于目的变量的信息量几多,和哪一个设置可以最小化所发生的猜测误差。
本文中的一切译文仅用于进修和交换目标,转载请务必注明文章译者、出处、和本文链接。
2KB翻译任务按照
CC 协议,假如我们的任务有进犯到您的权益,请实时联络我们。

2KB项目(www.2kb.com,源码交易平台),提供担保交易、源码交易、虚拟商品、在家创业、在线创业、任务交易、网站设计、软件设计、网络兼职、站长交易、域名交易、链接买卖、网站交易、广告买卖、站长培训、建站美工等服务
























